1. Types of gears
2. Gear arrangements
3. Considerations – Strength, speed, friction/noise/vibration
4. Layout Calculations
5. Hypocycloid
6. Differential planet
1) Types of gears
When looking at involute gears there are several categories of this type. Gear arrangements and types of gears are often used interchangeably but in my mind they are different. Lofting a gears dimensions to change the angle at which is attaches another gear does not make it inherently different to me .
Spur gears are easy and have the lowest tooth friction from rubbing friction.
Helical gears are stronger due to inclined teeth. Increased friction as teeth slide together but the transition is less dramatic and therefore smoother (noise, vibration)
Worm gears have the highest friction. Almost impossible to back drive. Properly designed can transmit high torque at significant reductions.
It’s fair to mention that each type of gear above can be designed simply or with great detail. A spur gear may be as simple as a wooden wheel nails in the radius. A worm gear may be a worm and helical meshed by single tooth or a throated worm gear. A helical can be mirrored into a herring bone. It goes on and on…
2. Gears can be arranged a variety of ways. Not much to add except there are numerous other layouts and arrangements and gear shapes. These layouts below are the most common. In each arrangement You will see variations in the cogs themselves that reflect the types listed previously.
Linear System
Compound
Bevel
Planetary
3. Design Considerations can become complicated quickly. Factors to consider are torque ratios, the speed at which the gears will operate, the loads they will encounter, the required lifespan, the noise or vibration created, the types of metals and friction coefficients. I’m going to focus on planetary gears after observing someone else’s work designing gearboxes.
4. Layout calculations
If a gear system already exist its very easy to calculate the reduction ratio. For example if two gears connect in linear and one has 25 teeth and the other 50 then its obvious that the small gear will need to turn 2 times to turn the big gear once. Or observing a worm gear you will see that one turn of the worm will move the worm wheel 1 tooth forward.
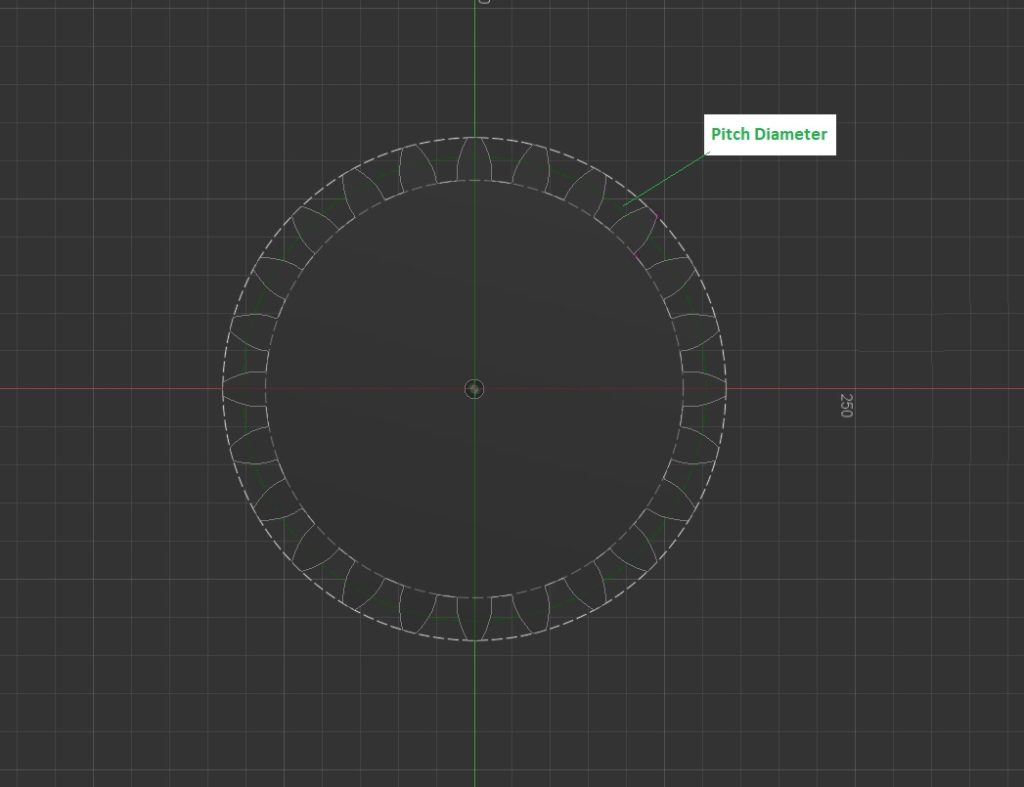
When lay outing out gears on you cad software you need to be precise. Lets start easy and work towards the planetary gear system. Gears can be drawn as circles based on their pitch diameter. When two gears mesh and interact they both meet at their pitch Diameter. Below its the green circle between the smaller(root diameter) and the larger (outside diameter) in white.
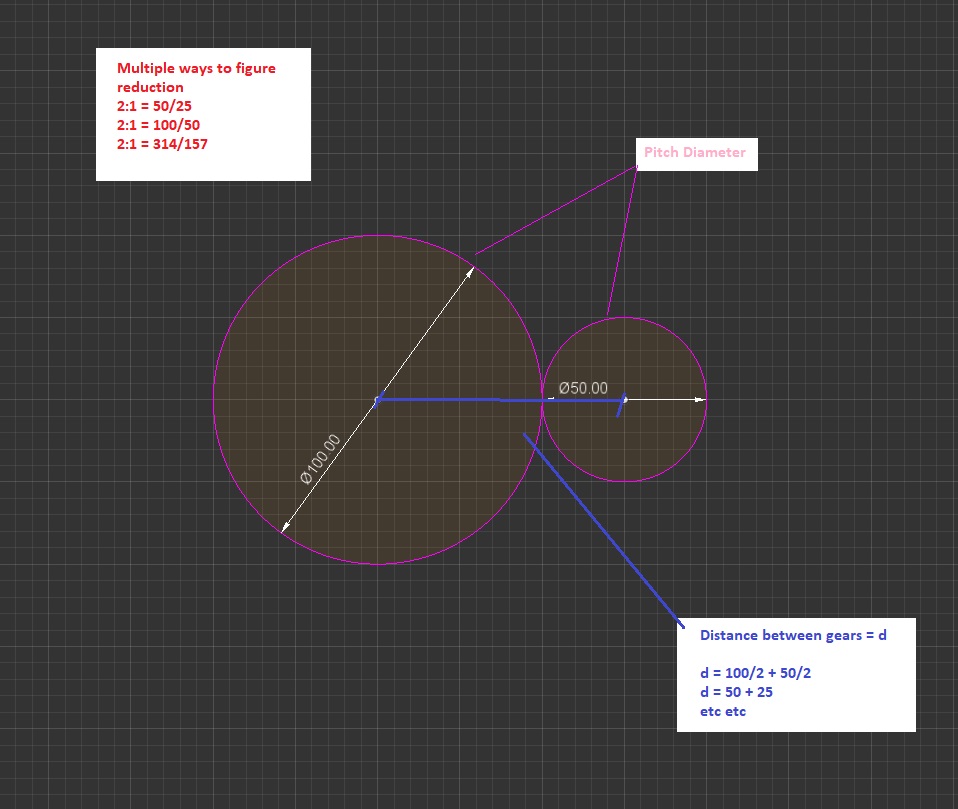
gear layout In order to figure out a gear reduction we get the radius of the pitch diameters and divide.
x/1 = R1/R2
So a 100 mm pd (pitch diameter) circle and a 50mm pd would be
2/1 = 50/25
Now the next question is how to actually place them adjacent to each other. We simply add both radius up and place center points that distance away.
One last important number is module. Module = pitch diameter/ # of teeth
There are other important names and references but they refer mostly to how the teeth interact. Briefly the most important 3 are…
Pressure angle = angle of top half of teeth
Clearance or backlash = extra spacing around teeth
Helix angle = helical gear cog/tooth angle
Based on the information above you could design a linear or compound system in cad fairly easily. But for a harder example let look at a planetary gear set. There is a lot to know about planetary gear sets but ill touch on the important starting points.
Planetary or epicyclic gears are similar to any linear gear arrangement except the are circular in arrangement. As seen below a center gear called a sun is surrounded by smaller gears called planets and then encased by a ring or annular gear.
These gears use the same spacing convention when designing in cad as linear gears. The use very similar reduction ratio math with two major differences.
First, the number of teeth on the planets is not used to calculate the reduction ratio. Add the sun gears number to the ring gears numbers to get conversion ratios.
Second, assume that 1 gear is drive gear, one gear is the load gear and one is fixed stationary.
So, imagine a gear as follows. Sun = 10 teeth, planets = 10 teeth(we will use 40), ring = 30 teeth. Using these number we make a fraction with the load gear as numerator and drive gear as denominator.
ratio = load/drive
Ring fixed and sun drive planets 40/10 = 4:1
planets fixed ring drives sun 10/30 = 1:3
The same math can be done using pitch diameter and circumference as shown in previous examples. Also consider if you could mechanically lock each of these gears or input/output force at will. You could get all sorts of interesting combinations on the fly similar to an automatic transmission.
There are other types of very interesting planetary gear systems.
Hypocycloid Gears
Here is an example gif that says it all.
Pitch diameter only plays a roll in the mechanical strength. Obviously there are ratios to maintain but to calculate reduction use this…
Ratio = (outter cogs/ cam cogs) – cam cogs
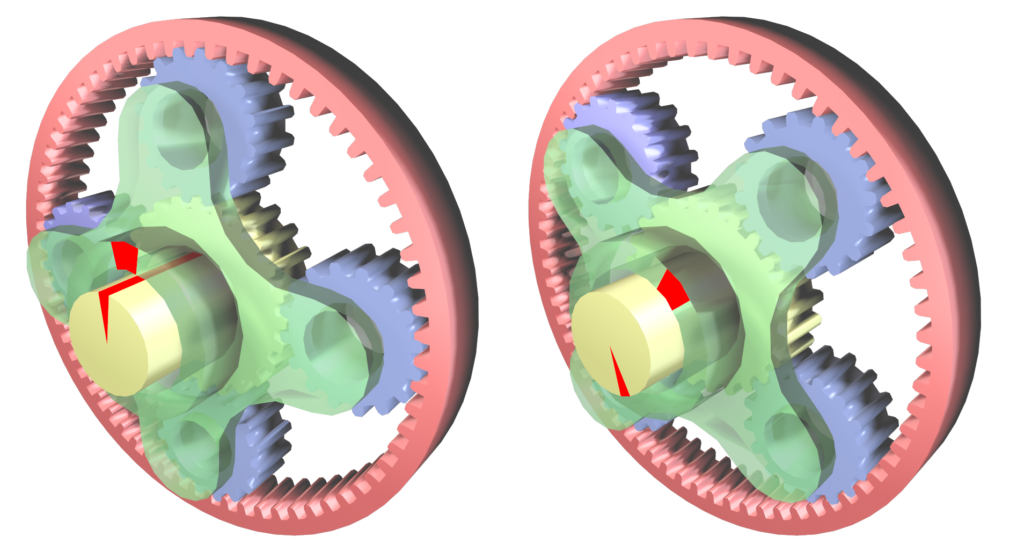
The example above has 11 outer cogs that look like white half circles and 10 inner cogs which are the yellow bumps. This gives a gear reduction of 10:1. Green is the power and purple is the output. These can also be stacked very efficiently such as below to create a differential cycloid. You can see pitch diameter is less relevant as angular velocity is the deciding factor as opposed to tangential velocity. The example below is the single cam in a motor mounting gear reduction box that produces a parallel or co-linear output.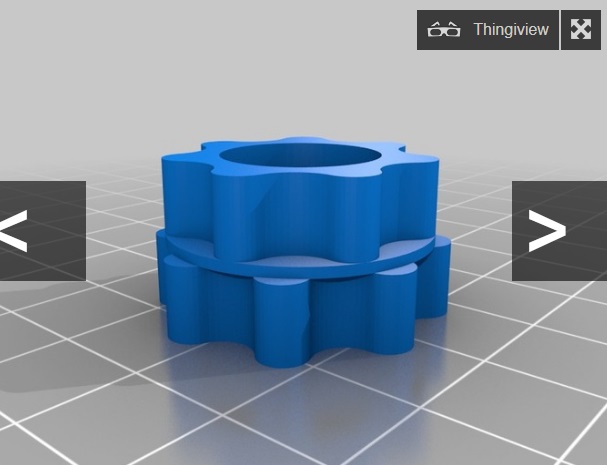
Calculating the difference in a differential hypocycloid is done as following. I consider the bigger cam the drive side.
drive = d, load = l, ring = r, cam = c
so… drive cam = dc and load ring = lr
ratio = 1/( 1-(dr*lc/ dc*lc))
There are a few scripts and editors for different software to create these. I did mine in fusion 360.
Differential Planet
Here is a cool gear design I found on thingiverse. The creator uses two planetary gears stacked with separate rings and suns and connected by their planets only. Each stack is geared differently.
Planets #1 Sun = 10 planets = 10 and ring = 30
Planets #2 Sun = 18 planets = 16 and ring = 50
Below is a front view and it works like a normal planetary gear. As expected with previous formula 40/10 is 4 turns of the sun causes the rotation of the planets once. The interesting part is the backside.
The backside is geared different from the front and this gives the back ring and additional 25:1 reduction ratio. On top of the 4:1 to one.
This is accomplished by creating a light difference between the front and back ring tooth count. The tangential velocity of the front planets are a perfect match to the front ring. But because the back ring is slightly different in size and the planet gears must move with the front sun gear the back ring is forced to move slightly forward or backward. Much like a tire slipping on a wet surface.
To make this easier to imagine imagine just the back ring. If the planet gear were unable to rotate the exterior ring would rotate 1:1 with the planets. Juxtapose the planets could rotate at the exact speed needed to keep the outer ring from moving. Then when you alter that speed even slightly you end up with a very string very slow gear ratio.
I never found an documentation but I tried to define it mathematically. All these refer to tooth but could probably be done with pitch diameter too.
D = drive ring, L = Load ring, S = Sun, P = Planet, R = annular ring,
LR/((LR/LP – DR/DP) * LP)/ ((DS+DR)/FS)
There may be an issue with this formula as it does no always match the reported gear ration of the device I’m measuring. Sorry for math styling, I do computer stuff so that’s how it should look to me!
Lastly there is also harmonic gear types. I did not do much research into these as the solutions above were suitable for my current needs. At this point the project I’m working on seems to moving forward but I would very much enjoy coming back to some of these gears designs and exploring more.